近日，我国科学家同时实现了机器学习和通信复杂度的量子优越性。
南京大学物理学院、固体微结构物理国家重点实验室、人工微结构科学与技术协同创新中心尹华磊、陈增兵课题组，首次实验证明了量子技术可以为机器学习提供具有量子优势的学习算法，并设计出量子版本的盲盒游戏，验证了量子优惠券理论的潜在应用价值。相关成果发表在美国《科学》(Science)杂志首个合作期刊《Research》。
图片来自《Research》机器学习可以从数据中提取有用的信息与知识，从而对基础理论、先进技术和社会生产力等方面产生重大影响。精确调控量子态技术在通信安全、计算速度和测量精度等方面已展现出超越经典技术的量子优势。通过利用量子技术来改进机器学习或实现量子机器学习是近年来研究热点，已有大量研究工作开展了创新性探索。
然而，此前的尝试大多为启发式的，并未从理论上证明量子机器学习比经典机器学习表现出更好的性能或拥有更短的训练时间。“可能近似正确”(PAC)学习理论量化了一个学习算法能够有效学习一个任务所需的最小样本数。因此，利用此理论研究量子机器学习，可为探索机器学习中的量子优势奠定理论基础。
2020年，荷兰阿姆斯特丹大学研究团队和美国IBM公司研究团队共同提出量子优惠券收集问题，并用PAC学习理论首次严格证明了该问题存在具有量子优势的学习算法。具体来说，所有希望学习到的目标函数所构成的集合称为“概念类”，并给定一个学习算法，它所考虑的所有可能映射的集合称为“假设空间”。若在PAC学习中，假设空间和概念类完全相同，即为恰PAC可学习(properly PAC learnable)，否则为不恰PAC可学习(improperly PAC learnable)。
一般来说，经典恰和不恰PAC可学习的样本复杂度是不一样的。然而，对于优惠券收集问题来说，恰和不恰PAC可学习所需的样本复杂度在量子算法下是可以相同的。因此，量子优惠券收集算法是首个依据PAC学习理论展现经典和量子机器学习之间存在根本性不同的算法。
优惠券收集问题，图片来自vcubingx原始的量子优惠券算法的实验演示需要用到高度复杂的单光子量子指纹态，以及远超当前实验技术的高度非线性测量装置，以实现超高维的半正定算子测量(POVM)。
此次，尹华磊、陈增兵课题组提出相干态量子优惠券协议，巧妙地将单光子量子指纹态转换为等效的相干态张量积形式，将单光子在维数上的振幅信息转换为相干态在时间箱上的相位信息，借此成功使用线性光学量子技术实验演示了量子优惠券收集任务，利用PAC学习理论，首次实验证明了量子技术可以为机器学习提供具有量子优势的学习算法。
团队从理论证明了相干态量子优惠券与原始量子优惠券在机器学习量子优势方面的等价性，从而实现了利用当前广泛使用的光量子通信技术（激光器、线性光学元器件和单光子探测器）来演示量子优惠券收集任务。
实验中需要最大限度地降低量子态干涉测量的噪声，包括：利用萨格纳克(Sagnac)干涉仪实现稳定的时间和相位对准；利用高精度的相位调制技术实现高速相位精确制备；利用高对称的保偏分数器实现偏振和强度对准；利用高效率和超低暗计数的超导纳米线单光子探测器实现近似完美测量。基于这些实验技术，团队最终清晰地演示了机器学习的量子优越性。
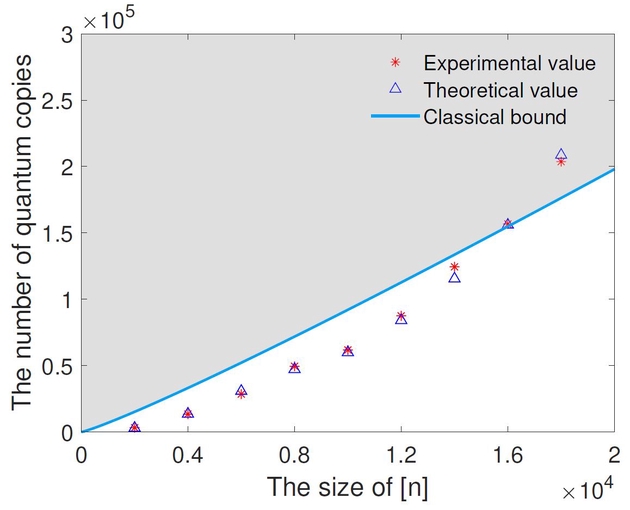量子优惠券实验结果图，图片来自南京大学物理学院为了进一步展示量子优惠券理论的潜在应用价值，团队针对年轻人喜爱的盲盒游戏，设计了其量子版本并成功进行了实验演示，充分展示了量子优惠券理论的潜在应用价值和量子技术在通信复杂度上的优势。
在盲盒游戏中，商家将不同图案的小球分别装进不同盒子里形成盲盒，并从中挑选几乎全部盒子作为盲盒套装，并制作了相同配置的多套盲盒套装。顾客只能在每套盲盒套装中抽取一个盲盒，来确认整套盲盒套装中所有小球的图案。顾客每消耗一套盲盒套装就需要支付一定数额费用，若顾客猜对，商家就会奖励给顾客奖金，奖金的数额为经典策略下所消耗盲盒套装费用的期望值。
使用量子资源对盲盒进行编码，顾客就可以通过设计量子编码和量子测量来降低自己的成本，从而在游戏中获得更多回报。量子优惠券实验结果表明，量子协议可以有效地减少学习具有多达14000个元素的优惠券所需的样本数量。量子盲盒游戏实验结果表明，针对不同类型的盲盒套装，顾客总可以通过选择合适的光强（发光强度）来降低成本以获得更多的回报，这说明量子优惠券协议在这种游戏中消耗的资源少于最优经典策略。
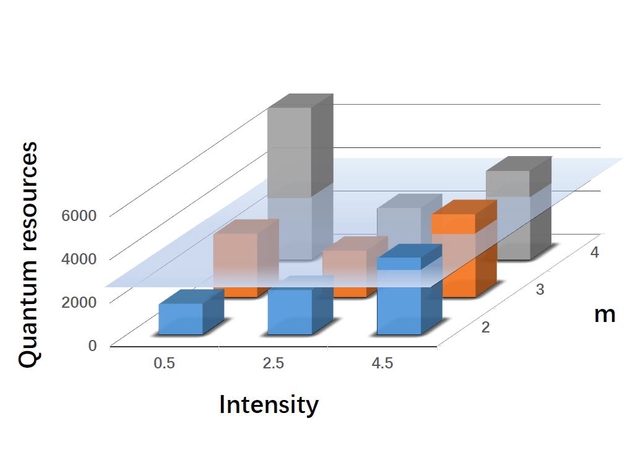量子盲盒游戏实验结果，图片来自南京大学物理学院前述实验结果有力证明了即使没有使用多粒子纠缠态和量子门操控，仅仅利用线性光学的量子技术，就可以在机器学习和通信复杂度方面，实现相对于经典技术的量子优越性。
论文共同第一作者为南京大学物理学院研究生周民罡、曹啸宇和陆玉硕，通信作者为南京大学副教授尹华磊和教授陈增兵。前述工作获得国家自然科学基金、江苏省自然科学基金、中央高校基本科研业务费、南京江北新区重点研发计划等支持。
