来源:原理
圆,是我们生活中最常见的形状。神奇的是,无论一个圆是像星球般大小,还是比原子更小,圆的周长与直径之比总是等于π(约等于3.14)。无论是在生活中,还是在揭开宇宙最深层次奥秘的公式中,我们都可以看到这一神奇的常数。
1、π的莱布尼茨公式

等式右边展开的无穷级数被称为莱布尼茨级数,或马达瓦级数。这个无穷的交替级数会收敛到π/4,它是逆正切函数展开式的一个特例,最早由印度数学家马达瓦于14世纪发现,并在17世纪70年代由莱布尼茨首次发表。仔细观察就能发现,这个公式将所有奇数与圆周率联系在一起,因此它也将数论与圆和几何联系了起来。通过这种方式,π连接了两个看似独立的数学世界。
2、巴塞尔问题

1+1/4+1/9+1/16+。。。这个无穷级数的求和问题被称为巴塞尔问题,它至少在1644年时就已经存在。几位著名的数学家都研究过这个问题,包括莱布尼兹,但他并没有找到精确解。直到1735年,欧拉精确地计算出了所有平方数(即1=1²,4=2²,9=3²,16=4²。。。)的倒数之和。
3、欧拉恒等式

欧拉恒等式联系了数学中最基本的五个数字,它被比作是莎士比亚的十四行诗,在许多人心中,这无疑是“最美公式”。
4、双曲几何中的三角形面积

双曲几何是非欧几里得几何的一种特例。它的一项显著的性质是,其三角形的内角α、β、γ之和总是小于180º。在几乎同一时间,俄国数学家巴罗切夫斯基与匈牙利数学家鲍耶发现,双曲几何中的三角形的面积可以通过π与内角和之差求得。
5、高斯-博内定理

高斯-博内定理是曲面微分几何中意义最为深远的结果之一,它是拓扑和微分几何之间的桥梁。它表明,闭合曲面的总曲率只与它的拓扑有关。该定理产生了各种各样强大的应用。
6、等周不等式

等周不等式也被称为等周定理,是几何中的一个不等式定理,它将欧几里得平面上的闭合曲线的边界长度l(周长)与其包围的面积A联系了起来。在所有闭合曲线所形成的形状中,圆形的面积最大,仅在此时等号成立。
7、π的倒数的无穷和表达式

与欧拉恒等式不同,拉马努金推导的这一极其复杂、繁绕的以无穷和的形式表达的π的倒数常被许多数学家调侃为“最丑”的数学公式。
8、爱因斯坦场方程

这一方程是爱因斯坦在1915年提出的广义相对论的核心方程。它说的是:引力 = 比例常数 ×(能量与动量)。简而言之,广义相对论可以总结为:时空决定了物质如何运动,物质决定了时空如何弯曲。
9、不确定性原理

海森堡的不确定性原理是量子力学的一个重要原理。粗略地说,它阐述的是我们无法同时绝对确切地知道一个粒子的位置和动量,其中一个属性被测量得越准确,对另一个的了解就越不准。但这一原理可延伸到粒子的其他某些物理属性对(被称为互补变量),例如时间长度和能量之间的关系也是以类似的不等式表示的。
10、黑洞温度
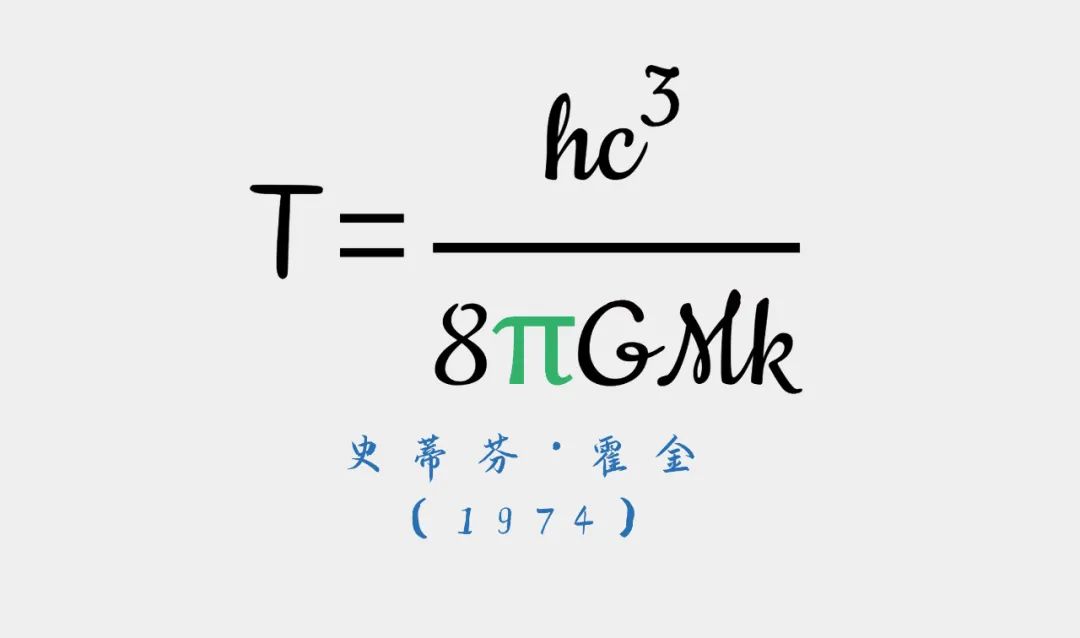
霍金在运用量子力学研究了黑洞邻近弯曲时空中的粒子后发现,黑洞具有温度(T)。而就像所有具有温度的物体一样,黑洞也能产生辐射,这种现象被称为霍金辐射。这一公式包含了牛顿的万有引力常数(G)、普朗克常数(h)、光速(c)、以及玻尔兹曼常数(k)。也就是说,霍金的工作把量子理论、广义相对论和热力学全部联系在了一起。
#创作团队:
撰文:原原
排版:雯雯
#图片来源:
封面图:NASA/JPL-Caltech
首图:NASA/JPL-Caltech