来源:机器之心
作者:魔王
这份讲义为初学者设计,涉及线性代数的基本概念、特殊矩阵及其应用,并提供了相应代码和图示。
人工智能的基础是数学,线性代数又是其中的重要部分。然而,对于数学基础不好的人来说,「线性代数」是一门非常抽象的课程。如何学习线性代数呢?这个 GitHub 项目介绍了一份入门级线性代数课程讲义,适合大学生、程序员、数据分析师、算法交易员等,使用的代码用 Python 语言写成。
项目地址:https://github.com/MacroAnalyst/Linear_Algebra_With_Python
讲义大致基于以下线性代数教科书:
1. Linear Algebra and Its Applications 作者:Gilbert Strang
2. Linear Algebra and Its Applications 作者:David Lay
3. Introduction to Linear Algebra With Applications 作者:DeFranza、Gagliardi
4. Linear Algebra With Applications 作者:Gareth Williams

该讲义为初学者设置,不过它对略有线性代数和微积分知识的人也有帮助。学习者应具备 Python、NumPy、Matplotlib、SymPy 的基础知识(3 天的训练足够了)。
为了使大家更容易地理解代码,讲义中涉及的所有代码均以直观的方式写成,而没有选择高效或专业的代码风格。
项目作者表示:这些讲义将为学习者提供数据学习、经济计量学、数学统计学、控制论等严重依赖线性代数的学科最需要的基础知识。耐心学习完之后,你将更好地掌握线性代数的基本概念,接下来就可以学习特殊矩阵及其应用。
讲义内容
这份讲义共包含 19 个章节,学习者可以使用 Jupyter NBViewer 打开 notebook,或者直接下载学习。
第一讲:线性方程系统
第二讲:基础矩阵代数
第三讲:行列式
第四讲:LU 分解
第五讲:向量运算
第六讲:线性组合
第七讲:线性无关
第八讲:向量空间与子空间
第九讲:基与维度
第十讲:行空间、列空间与零空间
第十一讲:线性变换
第十二讲:特征值与特征向量
第十三讲:对角化
第十四讲:动力系统的应用
第十五讲:内积与正交
第十六讲:Gram-Schmidt 正交化过程与 QR 分解
第十七讲:对称矩阵与二次型
第十八讲:奇异值分解
第十九讲:多变量正态分布
打开对应的 notebook 后,学习者可以看到对线性代数基本概念的讲解,以及代码和图示等。以第十二讲「特征值与特征向量」为例,下图展示了其几何直观图:
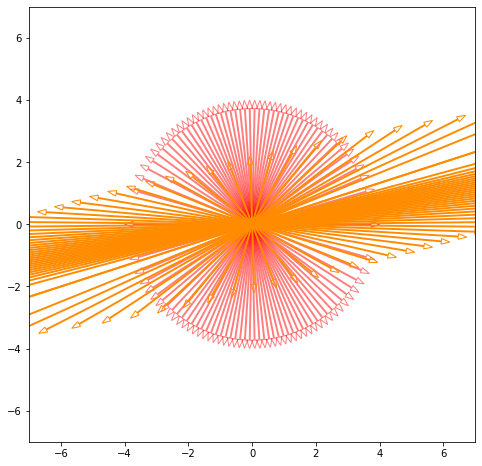
特征向量与特征值的几何图示。在线性变换前后方向相同的向量即为特征向量,其长度比为特征值。