图片来源：pixabay天气越来越热了，这个时候能舒舒服服冲个澡自然是再开心不过了。但是很多朋友都有过这样的经历：水龙头出来的水要么太凉要么太热，怎么也调不到满意的温度。要解决这个问题，就要涉及到我们今天要说的延迟方程了。
作者丨Chris Budd
翻译丨C&C
审校丨Dannis
相信大家都有过这样的经历：在淋浴时感觉水太冷了，所以你打开了热水龙头。但是水温不会马上变化——因为热水需要时间来流经管道——因此你最终会把温度调得更高。之后热水流过了管道，从花洒流到你身上。但是这时温度又太高了。于是你马上把热水龙头关上，但等到效果显现的时候，水又太冷了。所以你又得把温度调高。如此循环往复——似乎不可能调到正确的温度。
图片来源：pixabay有一个方程可以描述这种情况。从气候变化到COVID-19，这个等式的应用已经远远超出了浴室的范围。这是因为世界上的很多过程会涉及经过延迟才会产生的效应。但在讲述它的应用之前，让我们看一下这个方程。
我们写下在t时刻感受到的水的温度T(t)。假设水要花d秒的时间才能流过管道。那么淋浴方程便是
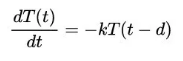（1）我们回顾下这个表达式。左边表示t时刻水的温度变化率，正值代表着t时刻水温增加，负值代表着t时刻水温降低。正值越大(或负值越小),在t时刻的温度升高(或降低)的速度越快。
方程的右边告诉我们：t时刻的变化率正比于t时刻之前d秒时的温度，也就是说，它正比于T(t-d)。这是有道理的：温度在t时刻的变化率取决于你在(t-d)时刻提高(或降低)多少热量，而这显然取决于你当时感觉水有多热或多冷。数字k是比例常数(我们假设它大于0)。
最后，这个负号反映了这样一个事实：(t-d)时刻的高温意味着你会调低温度，从而导致t时刻的温度降低；而(t-d)时刻的低温意味着你会调高温度，从而导致t时刻的温度升高。
好吧，这有一点不准确的地方：严格来说，这个方程告诉我们：如果温度低于0，你就会提高温度，如果温度高于0，你就会降低温度。这显然不太准确，因为仅仅高于0是远远不够温暖的。然而，我们可以很容易调整这个方程使得它反映这样一个事实：你可以用某个理想值（除0℃外)为参考点来调高或调低温度。
求解这个方程意味着找到满足它的函数T(t)。这个函数T(t)会给出任意t时刻的温度。充分了解这个函数后，你就会知道，开关热水龙头究竟是会保持一个舒适的温度，还是会让你一直开下去而得不到一个满意的结果。
由于我们的方程涉及到变化率，也被称为导数，所以这个方程被称为微分方程。这样的方程很少有容易求解的，但我们至少可以探索它的解是什么形式。这需要一点微积分知识。如果你还没有准备好，你可能想要跳到这篇文章的最后一部分，在那里我们将认识到淋浴方程的重要应用。
不含延迟
让我们先看看如果水穿过管道完全不需要时间会发生什么——这样就没有延迟：d=0。方程(1)变成
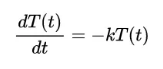
如果你知道一点微分你就会知道下面这个函数
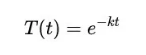
是这种情况的一个解。下面是这个函数的不同值的图。在任意一种情况下，我们看到温度的行为都是稳定的：它收敛到0值（前面提到，我们假设这是我们追求的理想温度）。
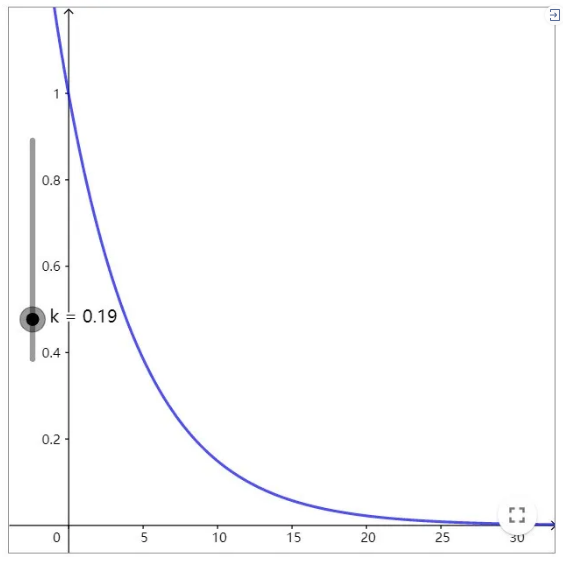kd=0.19时的图像含有延迟
当有延迟时，d就不等于0，这时候数学就变得困难了——你可以直接跳到文章的结尾，看看这个方程的应用。
假设解的形式是这样的
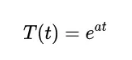（2）a是一个参数。我们的任务是找出参数a应该是怎样的。方程(2)对t求导得到
代入原方程(1)得到
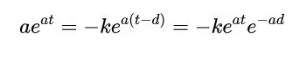
当参数a满足下面的超越方程时，此方程恰好成立。
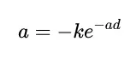（3）我们可以把它写成更整洁的形式：
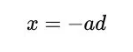
那么方程(3)变成
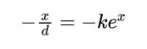
这样
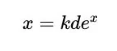
超越方程很难解，但我们能做的就是画出这两个函数，看看它们交点的情况。这些交点的横坐标x满足式(3)。如下所示（你可以点击图片进去使用滑块来改变(dk)的值）：
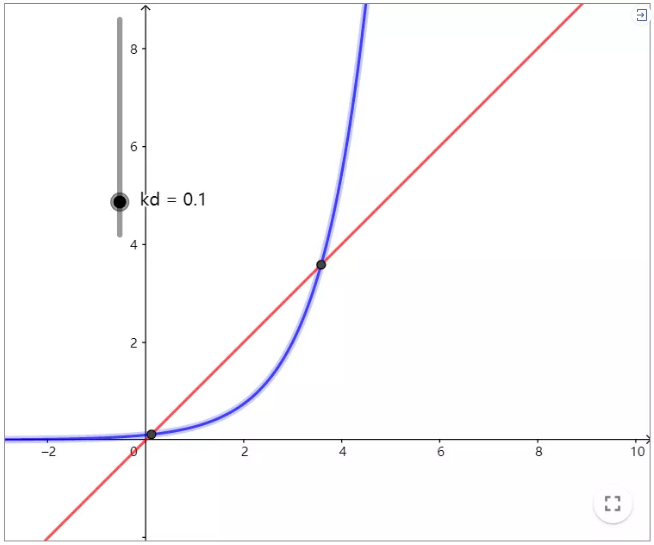kd=0.1时的图像从图中可以看出，方程(3)只有当时小于0.37左右的某个值时才有解。事实上，它只有当
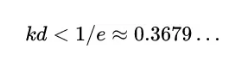
才成立。这里e是自然对数的底。
这种情况下的解x是正数。因为x=-ad和d也是正的（记住它表示延迟），这意味着a=-x/d是一个负数。
这样原始的淋浴方程(1)的解具有类似与无延迟的情况下方程解的形式：随着时间的推移，它将趋于0。换句话说，如果我们的延迟参数d和比例常数k的乘积小于或等于1/e，我们开关热水龙头最终会得到一个理想的温度。
如果kd>1/e将会发生什么呢？这时我们需要进入复数领域：这种情况下，方程(3)没有实数解，但它却有复数解。这里我们不详细讨论，但事实证明，如果这些复数解的实部小于0，淋浴的情况仍然是可控的：开关热水龙头最终会让我们达到所需的温度。
然而，如果复数解的实部大于0，那么淋浴就不可控制：温度将持续上升和下降——当然这就让我们很不爽。根据延迟参数d和比例常数k，这两种情况之间的转变发生在乘积(kd)等于π/2的时候。
气候变化与新冠肺炎
如果你跳过了数学部分，现在欢迎来到应用部分！我们在数学部分得到的结论是：
如果延迟参数和比例常数的乘积(kd)小于π/2，那么淋浴的情况是可控的:开关热水龙头最终会得到我们想要的温度。
当kd<1/e时，这一调节过程中温度不会有任何振荡；当1/e
下面的两个图说明了这一点。
kd=0.25<1/e情况下的温度函数
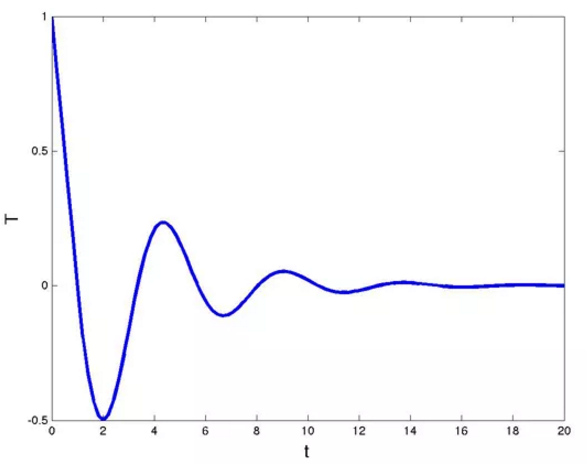
1/e
然而，如果kd>π/2，温度函数将继续剧烈振荡，如下图所示。
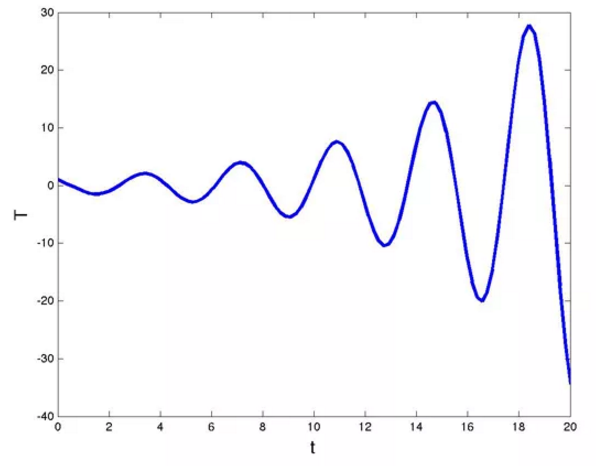kd=2>π/2情况下的温度函数现在，如前所述，让我们看看淋浴方程的其他应用。最重要的应用是对气候动力学的研究，因为许多气候现象需要时间才能产生影响。
例如，如果我们改变现在排放到大气中的二氧化碳量，那么我们需要等待一段时间，才能看到这对地球温度的实际影响。这使得很难确定二氧化碳减少的影响，并可能导致不受控制的振荡。
另一个例子是厄尔尼诺-南方涛动(El Niño Southern Oscillation，ENSO)。这是一种热带地区太平洋温度的不规则变化，升温事件周期大约为4年。厄尔尼诺现象不仅影响它出现的地区，而且对全球经济都有重大影响。如果我们能更好地预测它，那么这将有助于太平洋地区的国家和地区做好准备。
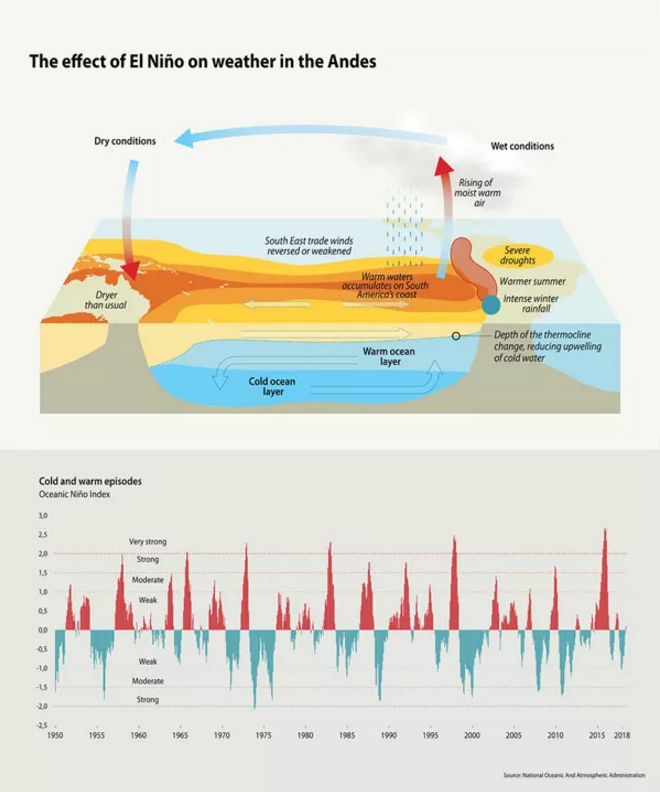厄尔尼诺对安第斯山脉天气的影响。RiccardoPravettoni绘制ENSO是由洋流和大气之间的相互作用引起的，它改变了海洋的温度。ENSO可以用一个和淋浴方程非常相像的方程来模拟。在这种情况下，延迟是洋流从南美洲西海岸到亚洲东海岸往返所需要的时间（见上图）。这导致了我们看到的周期性。事实上在这种情况下，方程包含额外的非线性项，这会导致混沌动力学叠加在周期振荡上。
我们的方程同样适用于理解农业对气候变化的反应。这也涉及到延迟，因为作物需要时间生长，这导致很难在变化的环境中规划何时种植和收获作物。
淋浴公式也与我们目前因COVID-19而出现的情形非常相关。回顾我们的众多举措，我们通过社交距离和接种疫苗实现了对疫情的有效控制，生产生活已经基本恢复正常。但事实上这些措施需要一段时间才能生效，所以我们要再次处理延迟的问题。此外，COVID-19的病毒潜伏期为5天至2周。在这段潜伏期内，没有明显的症状，所以从一个人被感染到明显生病之间有一段时间，这在模拟疫情时需要考虑。这直接导致了淋浴方程的不同版本，也就是所谓的包含了延迟和控制的SIR方程，可以用来帮助我们理解和控制流行病。就像ENSO系统一样，一旦方程中加入了延迟，事情就变得更加不确定。因此，(卫生和经济)系统的可控制性如何还有待观察。
原文链接：
https://plus.maths.org/content/shower-equation
