来源：中科院物理所
明天就是除夕了，要说起回家过年，那我可就不困了。每年过年回家后，只需要张口喊一声“妈~”，就能满足自己心中那股原始的干饭欲望。
有些在外工作的打工人朋友跟我说，他们决定今年不回家过年了，留在公司加班。不仅薅了老板的羊毛，还响应了国家“原地过年”的号召。
说到国家提倡的“原地过年”，其实背后是有着充分的科学依据的。我们今天就来聊一聊传染病的数学模型。
首先让我们来看看建立模型需要用到哪些参数吧！
01
人群分类
一般情况下将人群分为四类：易感者、暴露者、感染者、康复者，每类人的数量分别用大写字母S，E，I，R来表示。
S
易感者（Susceptible）：
尚未得病的人，由于缺乏免疫能力，与感染者接触后容易受到感染。
E
暴露者（Exposed）：
指接触过感染者，但不存在传染性的人，常用于存在潜伏期的传染病模型中。
I
感染者（Infectious）：
已经被感染，并且有传染他人能力的人，可以将疾病传播给“S“类人，使其变为”E“类或者”I“类成员。
R
康复者（Recovered）：
指被病愈后具有免疫力的人，如果是终身免疫性传染病，则不可重新变为“S”类、”E”类、”I”类人员；如果免疫期有限，就可以重新变为”S”类人，进而再次被感染。
除此之外，想要描述传染病的模型、建立方程还需要一些其他参数：β表示接触传染率，δ为潜伏期发病率，μ代表治愈率，总人口N；小写字母s，e，i，r代表某一类人占总人数的比例。
有了这些，接下来我们就可以开启建立模型的旅程啦~
02
三个简单模型
SI模型
适用范围：
SI模型适用于没有潜伏期，无免疫力，无治愈情况的疾病。感染者I通过接触将易感者转变为感染者。
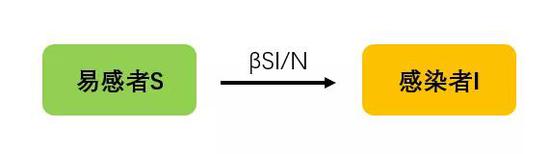
建立动力学微分方程，单位时间内，感染者每天增加数量与易感者比例、感染者人数、以及传染率正相关。同时，感染者增加了多少人，易感者就减少了多少人：
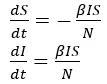
限制条件，总人口由易感者和感染者两部分组成：
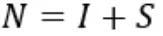
解方程得到：
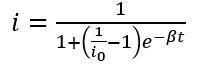
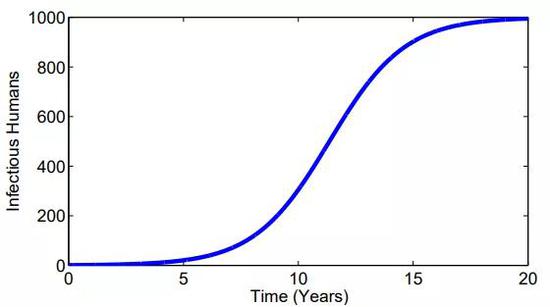图 | 感染者人数随时间变化（来源：参考文献[5]）随着时间t→∞，感染者比例 i 趋近于1，这意味着所有人都将被感染。
我们也可以把每一类人想象成一个储水槽，这样问题直接就简化成了小学应用题。S里的水源源不断流到I中，直到S中没有水了，所有的水全都转移到了I中。
SIR模型
适用范围：
SIR模型适用于无潜伏期，被治愈者终身免疫的疾病
建立动力学微分方程：
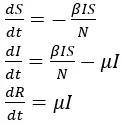
以及限制条件：
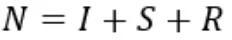
遗憾的是，这个方程没有解析解，只能在给定初始条件的情况下通过计算机进行数值求解，小编也无能为力。。。。。。
BUT！
我们仍然可以用小学水池排水注水来定性分析。与之不同的是，一旦I水槽中没水了（感染者消失），那么整个过程将立即停止。所以我们关注I水槽中的情况，易感者被感染类比成向I水槽中注水过程，感染者被治愈类比成I水槽向外排水过程。
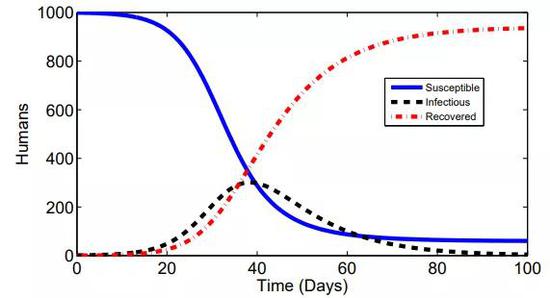图 | 情况①三类人数量变化曲线（来源：参考文献[5]）情况①：当注水量大于排水量时，所有水都会经过I水槽流入R水槽中。即所有人最后都会经过被感染后康复的过程成为康复者。
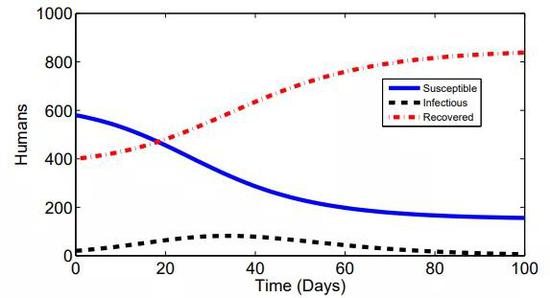图 | 情况②三类人数量变化曲线（来源：参考文献[5]）情况②：当注水量小于排水量时，I水槽里的水会随着时间的推移在某一时刻排干。这意味此时人群中不存在感染者了，那么整个注水排水过程将立即停止。最终，人群中会剩余一部分没有感染疾病的幸运儿，其余人都是经历了感染阶段的康复者。
emmm。。。。。。
SEIR模型
适用范围：
SEIR模型适用于存在潜伏期，治愈后获得终身免疫的疾病。
建立微分方程：
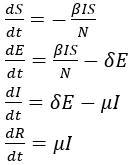
限制条件：
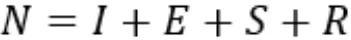
同样，这个模型也没有解析解，我们仍然可以利用小学水槽注水应用题来类比。。。。。。（打断施法）
那这里附上一张一般情况的各类人群比例走势图：
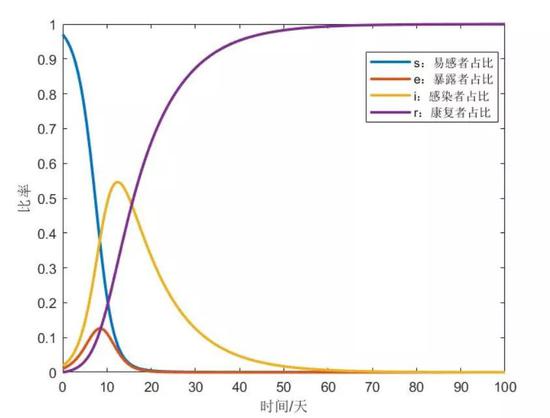图 | 四类人在人群中占比走势图（来源：小编 前进四）关于如何用小学数学题类比分析的问题就留给大家，欢迎大家在留言区把自己的思考分享给我们~
03
考虑人口流动的SEIR模型
上面我们介绍的这些模型，都是没有考虑人口流动的最最简单的单一群体模型。接下来我们再来看一个相对来说更加细致的，考虑人口流动的SEIR复合群体模型。
除了之前设置的参数外，还增设A为常数流动人口（设流动人口都是易感者），k为自然死亡率，α为因病死亡率。
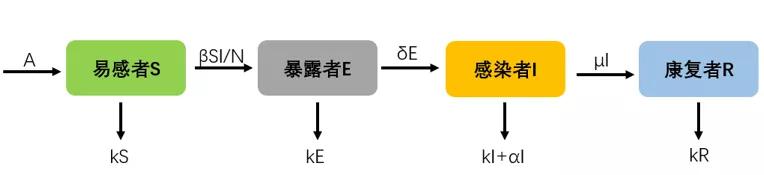
动力学微分方程：
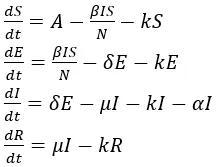
限制条件：
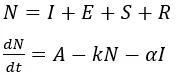
这个模型比较复杂，这里简要介绍一下结论，我们先引入一个基本再生数的概念：
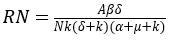
基本再生数RN（Basic Reproduction Number ）就好比一个开关：
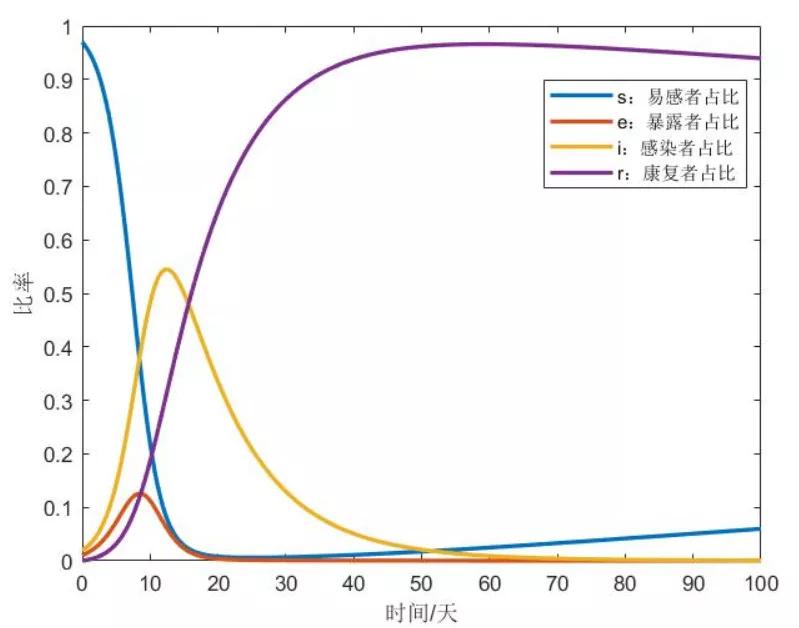图 | A/N较小，使得RN≤1时各类人群占比走势图（来源：小编 前进四）① 当系统参数使得RN≤1时，系统存在唯一的平衡点叫无病平衡点。顾名思义，随着时间的增加，最终疾病被消灭，人群中只有易感者和康复者。
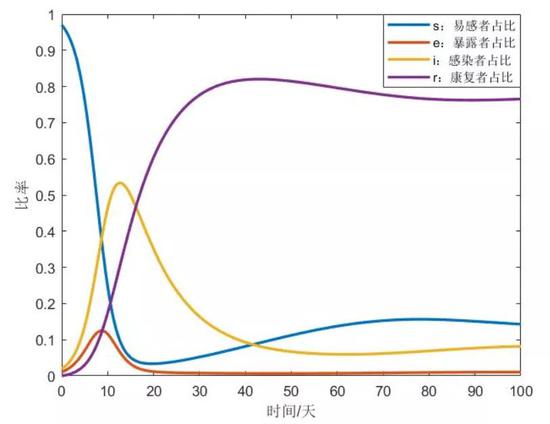图 | A/N较大，使得RN＞1时各类人群占比走势图（来源：小编 前进四）② 当系统参数使得RN＞1，存在唯一的平衡点叫做地方平衡点。这种情况下，疾病并不会消失，而是一直存在于人群之间。
对比上面两种情况不难发现，对于某一特定疾病来说，自然情况下的自然死亡率k，因病死亡率α，传染率β等参数一般来说不变。那么影响基本再生数的即为总人口N和人口流动数A。随着人口流动A的增加，RN将越来越大，当RN跨越1这个阈值的时候，系统中的疾病将一直存在下去。因此减少人口的流动，将更加有利于消灭疾病。而这就是我们国家提倡原地过年的科学依据！
相较于前面的基本的SEIR模型，这个考虑了人口流动的SEIR模型能更好的描述出新冠病毒特性。尽管有诸多因素没有被考虑进去，如：出生率，个体间差异，新冠病毒潜伏期也具备传染性等，但作为定性反映流动人口于病毒传播的模型也已经足够了。
如今，疫情还没有结束，小编建议亲爱的友友们平日里做好防护，减少出行。宅在家中刷刷剧、吃吃瓜；和家人们聊聊天、视视频，平平安安地度过春节。
最后，祝大家新年快乐！牛年吉祥！
