撰文 | Holger Müller
每一位物理学家都知道精细结构常数α的近似值(1/137)。这个常数描述了粒子物理标准模型中基本粒子之间电磁力的强度,因此是物理学基础的核心。例如,氢原子的结合能——即分开原子中电子和质子所需要的能量——大约等于电子质量所对应能量的α2/2倍。进一步地,电子的磁矩比带电的质点粒子的理论磁矩要略微大一些,即1 + α/(2π)倍。这个“异常”的磁矩已经在越来越高的精度下被验证成立,并成为了“标准模型最伟大的胜利”[1]。Morel等人在《自然》[2]上发表了一篇文章,以万亿分之81的精度测量了α的值。是此前最好测量结果的2.5倍[3]。
该测量包含了三个步骤。首先,使用一道激光束让原子吸收并释放多个光子。在此过程中,原子会发生反冲(见图1a)。原子的质量可以通过测量反冲的动能来计算。第二步,使用原子质量对电子质量的比例来计算电子质量[4,5],这个比例是已知的精确值(见图1b)。第三步,通过电子质量和氢原子结合能计算α,其中氢原子的结合能可以通过光谱学得出[6](见图1c)。
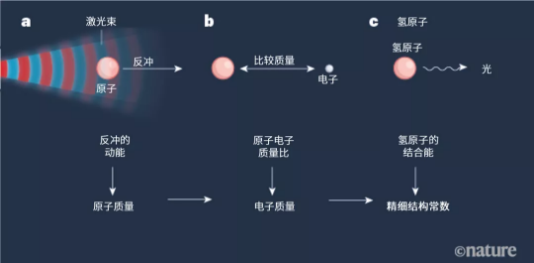
图1 | 测量精细结构常数的过程。Morel等人[2]发表了一种能以很高精度测量精细结构常数——反映基本粒子间电磁力强度的物理常数——的方法。a,测量该常数时,一束激光会引起原子反冲。图中的红色和蓝色分别表示光波的波峰和波谷。使用反冲的动能可以计算出原子质量。b,原子和电子质量的比值是有精确值的[4,5]。用这个值和原子质量就可以推导出电子质量。c,最后,电子质量和氢原子的结合能就可以用来计算精细结构常数。结合能可以通过光谱学技术[6],分析氢原子放出的光子来确定。
但是,反冲能量很小,难以测量。基于激光的原子冷却技术让物理学家能够对原子进行干涉测量——这一测量技术利用了原子物质波的干涉现象。在原子干涉仪中,原子有50%概率会和激光脉冲之中的光子发生相互作用。因此,氢原子同时存在于两个量子态中:静止的状态和吸收了光子动量后移动的状态。
这种情况相当于产生了两个反向传播的粒子物质波。这两道物质波可以通过发射更多的激光脉冲来重新组合到一起,并产生叠加或抵消的干涉效果,而这会导致观测到原子的概率变多或变少。两道干涉波之间的相位差与波的传播时间和反冲能量均成正比。
该测量手段之后又有了更多改进,能够支持更长的传播时间,并可以应对更多光子的相互作用。2011年,巴黎Kastler–Brossel实验室中开发出这一改进的研究组用这项技术以万亿分之660的精确度测量出了α的值[7]。翌年,他们测量了电子的异常磁矩,并推导出了精度为万亿分之250的α值[8]。2018年,我在加州大学伯克利分校的团队发表了一篇通过原子干涉测量计算α的论文,结果与之前的测量值相符,但精确度[3]提高到了万亿分之200。
现在,Morel等人将精确度提高到了万亿分之81。这是标准模型的又一个胜利,α的测量值和标准模型从异常磁矩中预测的结果一致,并且精度极高。这项结果证明了,例如,电子没有子结构,确实是基本粒子。如果电子是由更小的粒子组成,它的磁矩就会和观测结果不一样。
测量结果还缩小了某些暗区粒子的存在范围。这是一类可能存在的粒子,有些可能构成了暗物质——即宇宙中无法看到的那部分物质。在量子场论中,真空存在大量“虚拟”粒子,这些粒子会短暂存在然后消失。虚拟的暗区粒子会让电子的磁矩发生微小却可测量的改变。
但是,问题仍然存在。虽然每次测量出的α值和标准模型通过异常磁矩预测出的值差别很微小,但Morel等人的测量方法和前两组的测量方法并不太一致。正如论文[2]中图1所表示的,他们这篇文章是因为此前两组的测量值与标准模型的预测值不一致,并且一个大一个小。
作者提出,此前两组测量值之间的差别可能是因为散斑——激光强度在空间上的微小变化——或是由于电子信号处理中产生相位差。但是,之前的实验中是否有相位差已经无法测量了,而散斑会产生的测量值差异与实际发生的差异相反。
Morel等人也没有解释他们的结果与2018年实验之间的差距。这两项实验的差别在于原子-光子作用中使用的是铷还是铯原子,以及激光制备与准直的方法。这些不同的选择意味着环境对原子有着不同的影响。
例如,在两项实验中,最大的数据修正来源于激光。前文所述的散斑和光束的辐照度分布都会影响原子反冲的强度和方向。如果我的团队对这些效应修正过度,或是Morel团队修正不足,就可以解释结果之间的差异。最大的可能是,这需要进一步的实验结果来解释。
因此,实验物理学家正在想办法阐明该差异的来源,并再一次挑战标准模型。我的团队正准备建造一个可以最精确控制激光波形的原子干涉测量仪,以进一步提高α的测量精度。此外,对测量原子质量的改进也在进行中[5]。最后,西北大学正在开发测量电子异常磁矩的改进方法。[9]这些改进加在一起,可以让物理学家接近万亿分之10的精确度。在这个精度下就可以通过实验观测到τ轻子——电子的一种更重的兄弟,还可以探索很多尚是假设的暗区理论。
参考文献:
1.Gabrielse, G. Phys. Today 66, 64–65 (2013).
2. Morel, L., Yao, Z., Cladé, P. & Guellati-Khélifa, S. Nature 588, 61–65 (2020).
3.Parker, R. H., Yu, C., Zhong, W., Estey, B. & Müller, H. Science 360, 191–195 (2018).
4. Sturm, S. et al. Nature 506, 467–470 (2014).
5. Myers, E. G. Atoms 7, 37 (2019).
6. Udem, T. Nature Phys. 14, 632 (2018).
7. Bouchendira, R., Cladé, P., Guellati-Khélifa, S., Nez, F. & Biraben, F. Phys. Rev. Lett. 106, 080801 (2011).
8. Aoyama, T., Hayakawa, M., Kinoshita, T. & Nio, M. Phys. Rev. Lett. 109, 111807 (2012).
9. Gabrielse, G., Fayer, S. E., Myers, T. G. & Fan, X. Atoms 7, 45 (2019).
原文以Standard model of particle physics tested by the fine-structure constant标题发表在 2020年12月2日的《自然》的新闻与观点版块上
© nature
doi: 10.1038/d41586-020-03314-0
版权声明:
本文由施普林格·自然上海办公室负责翻译。中文内容仅供参考,一切内容以英文原版为准。欢迎转发至朋友圈,如需转载,请邮件[email protected]。未经授权的翻译是侵权行为,版权方将保留追究法律责任的权利。
© 2021 Springer Nature Limited. All Rights Reserved