来源:机器之心
编辑:小舟、陈萍
近日,Bourgain 截面问题与 KLS 猜想数学难题,被一位 90 后华人博士解决,并获得数学领域知名学者的赞扬。

比利时数学家 Jean Bourgain 于 1994 年获菲尔兹奖,以表彰他在巴拿赫空间、调和分析和遍历理论上的研究成果。他被认为是这个时代最具独创性、最敏锐的分析学大师之一。
20 世纪 80 年代中期,Jean Bourgain 提出了一个关于高维形状的问题,看似简单,却困扰了他数十年,未能解决。
 Jean Bourgain
Jean Bourgain最近这一数学难题被一位华人统计学博士攻克。成果一经发布,就迅速引起了数学、理论计算机科学、统计学等多个领域科学家的关注。
哈佛大学计算机科学教授、微软研究院前新英格兰首席研究员 Boaz Barak 发推祝贺。并表示这是一个非常重要的突破,加速了对近似凸体体积的研究。

困扰数学家多年之久的难题:Bourgain 截面问题
Bourgain 截面问题可以归结为以下简单问题:假设一个凸形的体积为 1,使用低一维的平面对该形状进行切割,得到的截面面积是否都极小,或至少有一个截面的面积特别大?
Bourgain 猜测存在面积很大的低维截面。特别是,他推测存在一个与维度无关的通用常数,使得每个形状都至少包含一个面积大于该常数的截面。
Bourgain 的猜想看起来似乎一定是正确的......
但证明该猜想的难点在于:高维形状中的情况往往与我们人类的低维直觉背道而驰。例如,在维度为 10 以上的情况下,可以建造一个立方体和一个球,其中立方体的体积比较大,但是每个穿过立方体中心的截面面积都比穿过球中心的截面小。
这一猜想不只困扰了 Bourgain 一个人,以色列魏茨曼科学研究所的研究员 Milman 与 Boáz Klartag 也在该问题上钻研了很长时间。
现在,Bourgain 的猜想被证明是正确的:华人统计学博士后 Yuansi Chen 在去年 11 月于 arXiv 上发表的论文《An Almost Constant Lower Bound of the Isoperimetric Coefficient in the KLS Conjecture》已经证明可以通过 KLS 猜想来解决 Bourgain 截面问题。

论文地址:https://arxiv.org/pdf/2011.13661v2.pdf
KLS 猜想
KLS 猜想是凸几何中最重要的猜想之一。这个有 25 年历史的猜想,是关于把一个形状切割成两等份的最佳方法,它蕴含了 Bourgain 的猜想。更重要的是,KLS 猜想是统计学和计算机科学中许多问题的核心,比如热量在凸形中扩散需要多长时间,或者一个随机游走者从一个起点走多少步才能到达一个真正随机的位置。
与 Bourgain 截面问题类似,KLS 猜想中也有一个简单的问题:假设你想将一个苹果切成大小相等的两部分,并且打算把它们放在一边以备后用。苹果内表面裸露在空气中会变成棕色,因此你要使其尽可能小。在所有可能的切口中,哪一个会最大程度地减少裸露的表面?
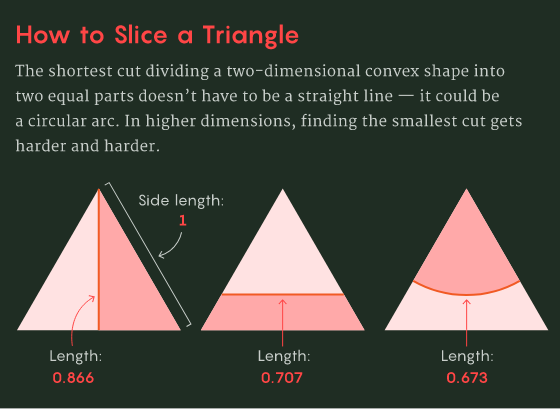
在这个问题中,苹果可以代表凸出的形状,如何能让截面的面积最小呢?由于很难确定最佳曲线切口,有三位研究者就想知道如果只允许直线切割,情况会有多糟糕。这三位研究者是 Ravi Kannan、László Lovász 和 Miklós Simonovits。1995 年,他们猜想:「即使只能用直线切割,情况也不会特别糟:存在一个通用常数,使得最佳平面切口的表面积至多等于整体最佳切割表面积的常数倍。」
虽然即使 Kannan、Lovász 和 Simonovits 无法证明他们的猜想,但正如佐治亚理工学院的 Santosh Vempala 所说:「这真是一个绝妙的见解。」三位研究者没有建立一个通用常数,而是建立一个因数,该因数可以近似计算形状所处维度的平方根。因此,例如对于一个 100 维凸形,他们知道最佳直线切割将最多暴露出最佳切割约 10 倍的表面积。
暴露 10 倍的表面积可能听起来并不是很好。但是,由于高维形状的许多属性都随维数的增长而呈指数增长,相比之下平方根的增长值是适度的。Bubeck 说:「这已经预示着高维中的情况没有很糟糕。」
但研究者们渴望改善这一结果。他们知道 KLS 因子包含了凸形内随机行为的信息,因为最佳切割越小,随机过程就越难在凸形的周围快速扩散。
例如哑铃这种物体,它由中间狭窄的桥连接两侧的两个球形。你可以将其划分为两个相等的部分,其中的桥梁只有一个小切口,这恰恰体现了桥梁是一种瓶颈的概念。一个球中的随机游走器通常需要很长的时间才能到达另一个球,因为它必须找到通过瓶颈的方式。
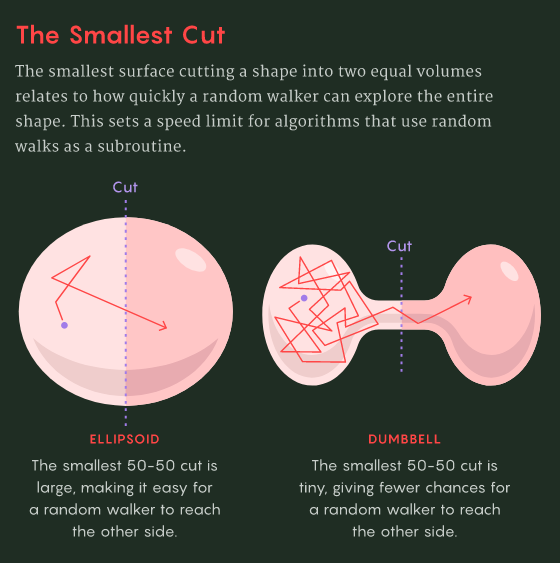
当然,哑铃不是凸的。哑铃可以有非常小的平面切口(例如从瓶颈切割) ,凸形做不到这一点,但凸形也许可以有非常小的弯曲切口。KLS 猜想本质上是在猜测高维凸形是否可以包含一种隐藏的、扭曲的哑铃?从而减慢随机混合的速度。
Kannan、Lovász 和 Simonovits 的平方根边界限制了这些隐藏哑铃的扭曲程度。2012 年,以色列数学家 Eldan 通过引入随机局部化(stochastic localization)技术降低了维度立方根的边界。
借助随机局部化的思想,可以很容易地证明 KLS 猜想是一个高度集中的团块,与哑铃几乎一样。通过证明倾斜对凸形没有很大的改变,Eldan 能够计算出原始形状的 KLS 边界。
几年后,华盛顿大学的研究员 Vempala 和 Yin-Tat Lee 完善了 Eldan 的随机局部化,将 KLS 的因数从维度的平方根降低到维度的四次方根。如果将维度称为 d,则平方根为 d^1 / 2,立方根为 d^1 / 3,四次方根为 d^1 / 4。通过提出一种称为 bootstrapping 的新方法,Lee 和 Vempala 认为他们可以将 KLS 边界一直降低到 d,为其升至 0 次幂加上一点 fudge factor。由于 d^0 始终等于 1,因此认为边界大致是一个常数。
 Yin-Tat Lee(左),Santosh Vempala(右)
Yin-Tat Lee(左),Santosh Vempala(右)Lee 和 Vempala 在网上发布了他们的论文。但几天后就被发现其中存在一个漏洞,推翻了他们对 d^0 边界的证明。Lee 和 Vempala 迅速发布了修订后的草稿,重新调整到 d^1/4 边界。几年来,研究者们一直认为这就是 KLS 故事的终结。
研究新突破:采用递归方法来降低 KLS 界限
Lee 和 Vempala 论文引起了华人博士后 Yuansi Chen 的注意,当时他还是加州大学伯克利分校的一名统计学研究生,正在研究随机抽样方法的混合率。而随机抽样是许多统计推断中的关键,例如贝叶斯统计。
Lee 和 Vempala 的论文向 Chen 介绍了随机局部化的概念。Chen 深入研究论文,花了数周时间试图填补 Lee 和 Vempala 证明中的空白,但无济于事。
在接下来的几年中,关于如何修改随机局部化的想法会定期出现在他的脑海中,他会思考几个小时然后放弃。最后,基于 Lee 和 Vempala 的 bootstrapping 方法,Chen 提出使用递归方法来降低 KLS 边界。其理论是:如果你可以让边界非常小,那么就有方法让边界更小。经过反复应用,这种 bootstrapping 方法为 KLS 猜想以及 Bourgain 截面问题实现了近似恒定的边界。
Chen 的研究结果显示,凸形的最佳对半切口并没有比最佳的平切口要小很多;也就是说,高维凸形不包含带有非常窄的桥梁的隐藏哑铃。
从实际的角度来看,这意味着随机游走在凸形中的混合速度要比研究人员之前证明的快得多。除此之外,这种理解将有助于计算机科学家在不同的随机抽样技术之间进行优先排序——找出最基础的随机游走何时是最好的,以及更复杂但计算成本更高的算法在何时会表现更好。
当 Chen 将论文上传到 arXiv 上后,便引起了数学家 Klartag 的关注。Klartag 提到:Chen 的论文非常容易验证,可以说是 100% 正确。
 数学家 Bo’az Klartag
数学家 Bo’az Klartag数学家们一致认为,Bourgain 会因为这项研究而激动不已,就在他 2018 年去世前几个月,仍时常询问截面问题是否已有进展。他在这个问题上花费了将近一生的时间,但都没有解决。令人意外的是,最后这个问题利用统计学解决了。
Yuansi Chen

Yuansi Chen ,本科就读于法国巴黎综合理工学院应用数学专业,2019 年从 UC 伯克利获得统计学博士学位,其博士生导师是著名华裔统计学家、UC 伯克利统计系和电子工程与计算机科学系终身教授郁彬。Yuansi Chen 目前在瑞士数据科学基金会(ETH Foundations of Data Science)担任博士后。
Yuansi Chen 的主要研究方向是统计机器学习、优化以及在神经科学中的应用,尤其对域适应、稳定性、MCMC 采样算法、卷积神经网络和计算神经科学中出现的统计问题感兴趣。他将在今年春季加入杜克大学统计科学系担任助理教授。
个人主页:https://people.math.ethz.ch/~chenyua/